多元线性回归的代价函数推导

共计 303 个字符，预计需要花费 1 分钟才能阅读完成。

决策函数：

hθ​(x)=θ1​x1​+θ2​x2​+…+θn​xn​=∑i=1n​θi​xi​=θTx

令有m个样本，对于每个样本：

y(i)=hθ​(x(i))+ϵ(i)…(1)

ϵ(i)表示真实值与预测值之间的误差,我们通常认为ϵ(i)是独立并具有相同的分布，并且服从均值为0方差为θ^2的高斯分布。

于是：

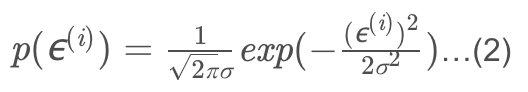
将(1)代入(2)可得：

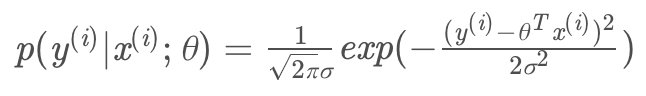
故似然函数为：

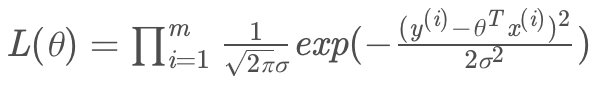
为方便求导变为对数似然：

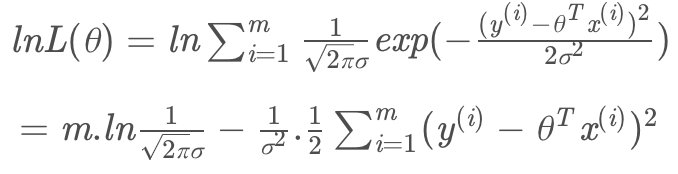
此时我们需要求得参数θ^使似然函数L(θ)最大：

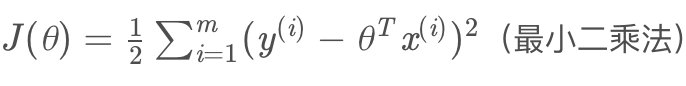
由化简后的式子可知，上式越小，似然函数越大

将代价函数写为：

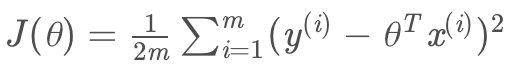
方便计算

参考：

https://blog.csdn.net/qq_39494028/article/details/81611217